参考文章: FPS通用的方框透视公式的原理_fps透视原理-CSDN博客
FPS游戏方框透视基本原理_fps 透视矩阵算法-CSDN博客
之前我们做的非矩阵画线,位置不准确,还很难进行缩放
但是下图是矩阵的效果,看上去就非常的好
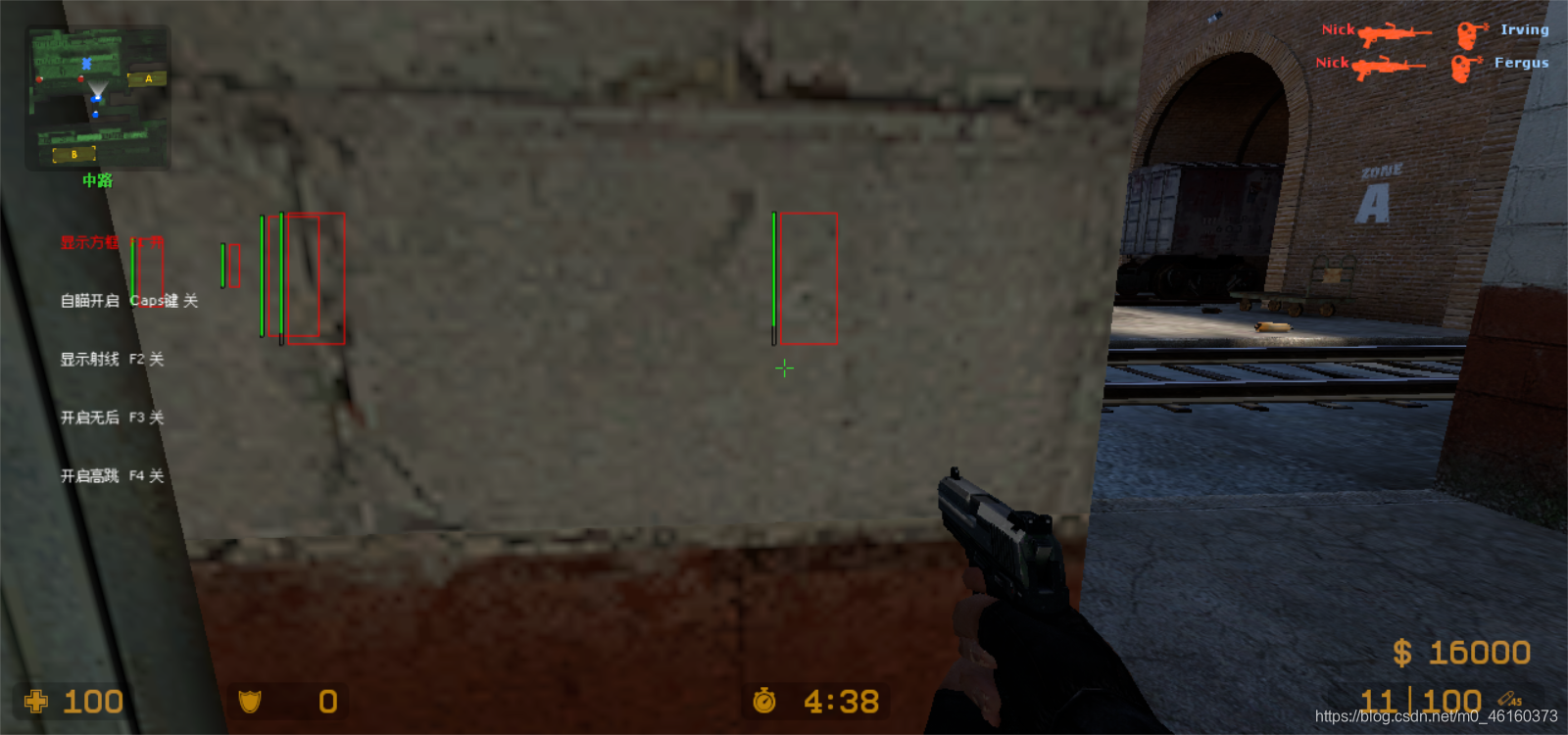
游戏坐标转换原理:
游戏中通过建模完成的3D物体要想在2D屏幕上显示出来需要进行坐标的转换。
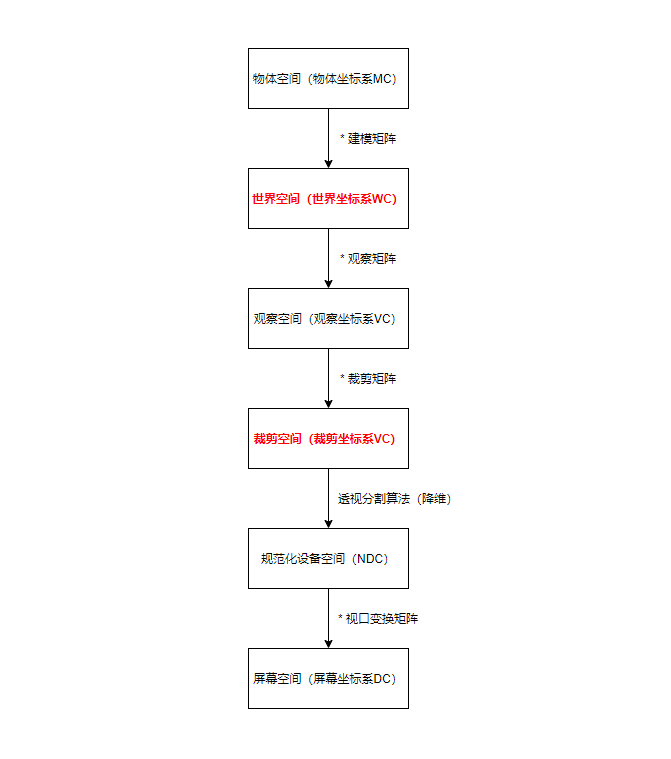
具体过程看 FPS游戏方框透视基本原理_fps 透视矩阵算法-CSDN博客 吧(看得我十分头大,不过我们只需要大概了解即可)
按照上面的原理,我们只要找到人物在世界坐标系中的坐标 (x1,y1,z1) ,就可以在屏幕上画出人物边框
第一步:世界坐标 -> 裁剪坐标
z1后面的那个1是w,为了兼容4*4矩阵
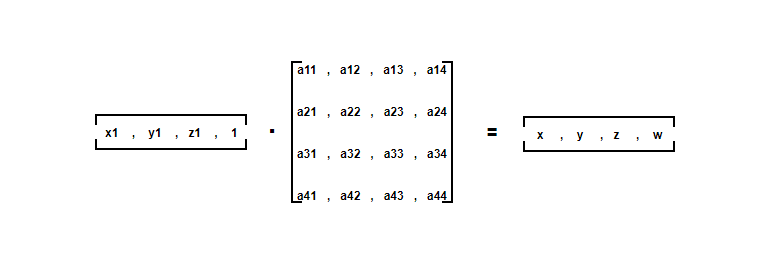
X = a11*x1 + a12*y1 + a13*z1 + a14
Y = a21*x1 + a22*y1 + a23*z1 + a24
Z = a31*x1 + a32*y1 + a33*z1 + a34
W = a41*x1 + a42*y1 + a43*z1 + a44
//(x, y, z)就是(x1,y1,z1)对应的裁剪坐标
//注意w有可能小于0,如果w小于说明物体不在你的视角范围中(不需要在屏幕上显示)。裁剪坐标 ----> NDC坐标
NDC坐标就是将裁剪坐标对应的xyz除以w,这就是透视分割算法(降维)。
NDC_X = X / W
NDC_Y = Y / WNDC坐标 ----> 屏幕坐标
这需要一个视口变换矩阵,视口变换矩阵左乘NDC坐标就会得到对应的屏幕坐标。其中视口变换矩阵中fs和ns一般为0。
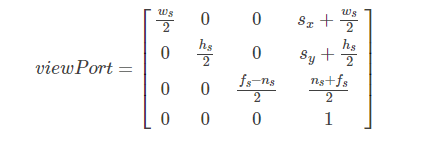
最后得到屏幕坐标的X = (Ws / 2 NDC.x) + (NDC.x + Ws / 2), Y = -(Hs / 2 NDC.y) + (NDC.y + Hs / 2)。而Ws * Hs为当前屏幕窗口的分辨率,且注意在windows中屏幕坐标系的规则
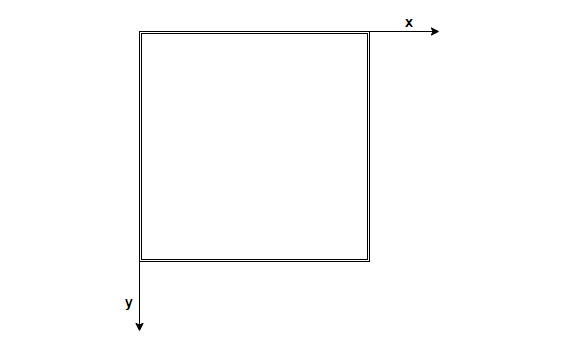
我们需要找什么矩阵
在开发FPS游戏的辅助工具(俗称“外挂”)时,“找矩阵”通常指的是找到与游戏中物体或玩家视角相关的变换矩阵。这些矩阵可以是Direct3D(D3D)或OpenGL中用于渲染场景的矩阵。
D3D矩阵和OpenGL矩阵 包括了用于计算相机视角的所有变换矩阵:
世界矩阵(World Matrix):将物体从局部坐标系转换到世界坐标系。
视图矩阵(View Matrix):将世界坐标系转换到相机坐标系。
投影矩阵(Projection Matrix):将相机坐标系转换到屏幕坐标系,并决定了FOV。
其实我们要找的就是相机FOV的矩阵,然后这个矩阵是通过D3D矩阵或openGL矩阵将一个坐标矩阵变换而来,最终得到一个相机FOV的矩阵
其中: D3D矩阵 是行主序
a00, a01, a02, a03,
a10, a11, a12, a13,
a20, a21, a22, a23,
a30, a31, a32, a33, //行主序openGL矩阵 是列主序
a00, a10, a20, a30,
a01, a11, a21, a31,
a02, a12, a22, a32,
a03, a13, a23, a33, //列主序 介绍找到的矩阵特性:
缩放和位移矩阵:
Sx 0 0 Tx
0 Sy 0 Ty
0 0 Sz Tz
0 0 0 Tw这样,一个坐标矩阵 ( x y z w )
乘上这个坐标矩阵之后就会得到
( Sx x + Tx w Sy y + Ty w Sz z + Tz w Tw*w )
)
缩小放大S倍,移动就用T * w表示
在FPS游戏中,角色的运动如走路、跳跃等,实际上会引起摄像机视点的变化。这个变化体现在位置的变换上,而位置的变换就体现在矩阵的最后一列。
结论1
所以得出结论: 行主序的最后一列,列主序的最后一行,在走路 跳的时候会改变(不代表其他动作不改变)
注意注意,貌似单纯跳,直走之后改变三个值,但是如果混合运动,就会四个值一起改变,这个也可以作为特征
旋转矩阵:
注意一下,以下说的xyz轴,都是以人物建立坐标系,不是世界坐标系
这是在xyz坐标系中的xy平面进行旋转,也就是绕着z轴旋转
cosA -sinA 0 0
sinA cosA 0 0
0 0 1 0
0 0 0 1乘上 坐标列矩阵 ( x y z w ) (右乘)
可以得到:
( cosA x - sinA y sinA x +cosA y z w
)
例如下面的转换
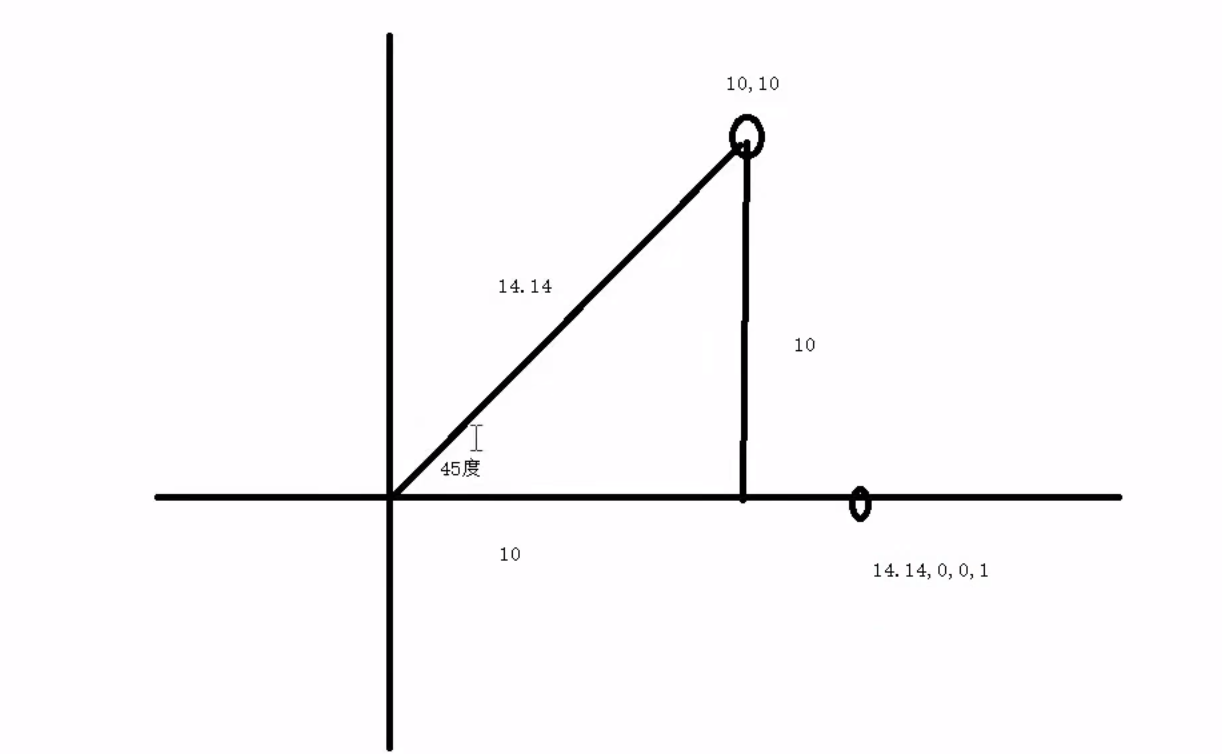
同理还有绕着x轴,y轴旋转
那么旋转矩阵就变为
//绕x轴旋转
1 0 0 0
0 cosA -sinA 0
0 sinA cosA 0
0 0 0 1
//绕y轴旋转
cosA 0 sinA 0
0 1 0 0
-sinA 0 cosA 0
0 0 0 1结论2
因此我们又得出一个结论:
在水平转动的情况下,也就是绕着Z轴旋转,行主序的第三列不变,列主序的第三行不变
同理
结论3:
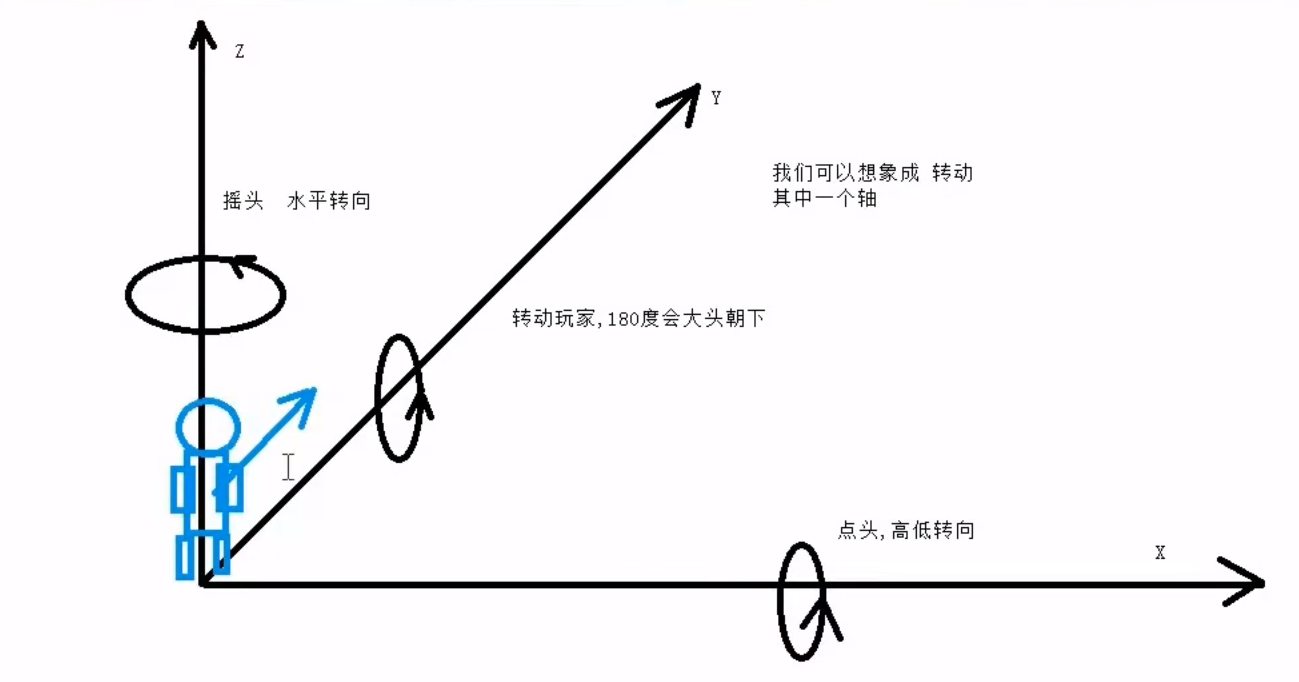
在高低朝向改变的时候,其实就是绕着x轴进行旋转
所以结论:
高低朝向改变的时候,行主序的第一行不变,列主序的第一列不变
其他结论:
很多的FPS游戏的规律:矩阵4*4的第一个值是-1到1,这是和引擎的特性有关(不一定)
行主序的第一行第三个元素是固定的0,列主序的第一列的第三个元素是0 (可能也不一定)
开倍镜的情况下,矩阵4*4的第一个值会乘相应的倍数(大概率对)
合集:
行主序的最后一列,列主序的最后一行,在走路 跳的时候会改变(不代表其他动作不改变)
在水平转动的情况下,也就是绕着Z轴旋转,行主序的第三列不变,列主序的第三行不变
高低朝向改变的时候,行主序的第一行不变,列主序的第一列不变
很多的FPS游戏的规律:矩阵4*4的第一个值是-1到1,这是和引擎的特性有关(不一定)
行主序的第一行第三个元素是固定的0,列主序的第一列的第三个元素是0 (可能也不一定)
开倍镜的情况下,矩阵4*4的第一个值会乘相应的倍数(大概率对)
找矩阵实践:
先说结论:
cstrike.exe+1820100 //矩阵基地址其实就是应用上述的结论,主要是结论1 结论2 结论3和最后一个开镜矩阵的第一个值会放大
值得注意的是,一开始我咋也找不着,因为我直接根据开镜第一个值就变大,不开镜就变小的结论去找
但是我忽略了一点,就是第一个值有可能是一个负数,这样开镜的话,乘以一个倍数就会变得更小,但是我仍然按照增大的值去搜,导致一无所获,这也算是学了个教训吧
还有其他技巧,就是原地跳,那么结论1的第一个值是不会变的,还有改朝向,只要是人物朝向和世界坐标的x y轴重合,那么直走的时候,结论1的第一个值也是不会变的
坐标转换:
世界坐标->剪辑坐标
拿世界坐标矩阵
x y z w去乘以我们刚刚找到的矩阵
a0 a1 a2 a3
a4 a5 a6 a7
a8 a9 a10 a11
a12 a13 a14 a15
也有可能是列主序
a0 a4 a8 a12
a1 a5 a9 a13
a2 a6 a10 a14
a3 a7 a11 a15 得到结果:
剪辑坐标x=a0*x+a4*y+a8*z+a12*w
剪辑坐标y=a1*x+a5*y+a9*z+a13*w
剪辑坐标z=a2*x+a6*y+a10*z+a14*w
剪辑坐标w=a3*x+a7*y+a11*z+a15*w
剪辑坐标x=a0*x+a1*y+a2*z+a3*w
剪辑坐标y=a4*x+a5*y+a6*z+a7*w
剪辑坐标z=a8*x+a9*y+a10*z+a11*w
剪辑坐标w=a12*x+a13*y+a14*z+a15*w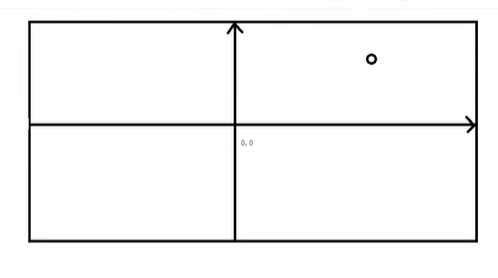
此时将世界坐标转换为了二维平面的坐标,但是和设备的分辨率没啥关系,需要进一步变换
剪辑坐标->NDC坐标:
NDC.x = 剪辑坐标x/剪辑坐标w
NDC.y = 剪辑坐标y/剪辑坐标w
NDC.z = 剪辑坐标z/剪辑坐标w把剪辑坐标变成范围限定在-1~1
NDC坐标->屏幕坐标:
NDC.x/1=屏幕坐标差.x / (分辨率_宽/2)
NDC.y/1=屏幕坐标差.y / (分辨率_高/2)所以我们可以推出来:
屏幕坐标.x = 屏幕坐标差.x + 分辨率_宽/2
(分辨率_宽/2)*NDC.x + 分辨率_宽/2
屏幕坐标.y = -屏幕坐标差.y + 分辨率_高/2
-(分辨率_高/2)*NDC.y + 分辨率_高/2 额外加一个 分辨率 宽/ 2 , 分辨率高/2 是因为NDC坐标原点在屏幕中心
还有在NDC坐标系中,一二象限的y是正值,三四象限是负值,但是我们的屏幕坐标从上到下是增加的。所以我们需要自己加一个负号
世界坐标转为屏幕坐标代码实现:
bool 绘制::世界坐标转为屏幕坐标_矩阵(对象结构 目标对象结构, 屏幕坐标结构& 目标屏幕坐标结构)
{
for (int i = 0; i < 16; i++)
{
矩阵[i] = *(float*)(矩阵地址 + 4 * i);
}
DWORD w = 1;
float 剪辑坐标x = this->矩阵[0] * 目标对象结构.对象重心的x坐标 + this->矩阵[4] * 目标对象结构.对象重心的y坐标 + this->矩阵[8] * 目标对象结构.对象重心的z坐标 + this->矩阵[12] * w;
float 剪辑坐标y = this->矩阵[1] * 目标对象结构.对象重心的x坐标 + this->矩阵[5] * 目标对象结构.对象重心的y坐标 + this->矩阵[9] * 目标对象结构.对象重心的z坐标 + this->矩阵[13] * w;
float 剪辑坐标z = this->矩阵[2] * 目标对象结构.对象重心的x坐标 + this->矩阵[6] * 目标对象结构.对象重心的y坐标 + this->矩阵[10] * 目标对象结构.对象重心的z坐标 + this->矩阵[14] * w;
float 剪辑坐标w = this->矩阵[3] * 目标对象结构.对象重心的x坐标 + this->矩阵[7] * 目标对象结构.对象重心的y坐标 + this->矩阵[11] * 目标对象结构.对象重心的z坐标 + this->矩阵[15] * w;
if (剪辑坐标w < 0.0f)
{
目标屏幕坐标结构.x坐标 = 分辨率_宽 / 2;
目标屏幕坐标结构.y坐标 = 分辨率_高 * 3 / 4;
return false;
}
float NDC_x = 剪辑坐标x / 剪辑坐标w;
float NDC_y = 剪辑坐标y / 剪辑坐标w;
目标屏幕坐标结构.x坐标 = (分辨率_宽 / 2) * NDC_x + 分辨率_宽 / 2;
目标屏幕坐标结构.y坐标 = 0-(分辨率_高 / 2) * NDC_y + 分辨率_高 / 2;
return true;
}
